The Band Structure Of Solids
We restrict ourself two one-dimensional solids for simplifications. The potential energy of the delta function molecule for a solid is:
![Rendered by QuickLaTeX.com \[\frac{2mV(x)}{\hbar^2}=\frac{\alpha}{a}\sum_{n=1}^N\delta(x-na)\]](http://bootcampforscience.com/wp-content/ql-cache/quicklatex.com-49b1ea45c997b950afc803b3d45abdf8_l3.png)
where ![]() is the separation between each of the delta function,
is the separation between each of the delta function, ![]() is a dimensionless parameter, and
is a dimensionless parameter, and ![]() is the number of atoms in the one dimensional model. Solving the Schrödinger equation directly involves working within a large number of regions between these delta functions.
is the number of atoms in the one dimensional model. Solving the Schrödinger equation directly involves working within a large number of regions between these delta functions.
Instead of solving the equation in each region individually, we use Bloch’s ansatz.
![]()
Note that:
![]()
We presume that:
![]()
The type of boundary condition typically refer to as a periodic boundary condition and requires:
![]()
which is satisfied if:
![]()
or
![]()
Each allowed value of ![]() differs from the adjacent one by a factor of
differs from the adjacent one by a factor of ![]() . Since the number
. Since the number ![]() atoms in a solid is very larger, the allowed values of
atoms in a solid is very larger, the allowed values of ![]() are discrete but very closely spaced. There are
are discrete but very closely spaced. There are ![]() distinct values of
distinct values of ![]() , ranging from
, ranging from ![]() to
to ![]() . Note that when
. Note that when ![]() ,
, ![]() and
and ![]() , which is the same as
, which is the same as ![]() and
and ![]() , so
, so ![]() .
.
Suppose ![]() . The allowed values of
. The allowed values of ![]() are:
are:
![]()
This gives:
More explanation with an example
– ![]() for
for ![]()
– ![]() for
for ![]()
– ![]() for
for ![]()
– ![]() for
for ![]()
Now, if ![]() , we get
, we get ![]() for
for ![]() . Then,
. Then,
![]()
which is the same as
![]()
For other ![]() values, however
values, however
![]()
We write the Schrödinger equation in those regions in which ![]() , giving us:
, giving us:
![]()
The general solution is:
![]()
To handle multiple regions between potential barriers, the wave equation is written in adjacent regions with shifted coordinates. For the region between ![]() and
and ![]() , we have
, we have
![]()
For the next region between ![]() and
and ![]() , we have:
, we have:
![]()

The Bloch’s theorem states that the wave function repeats with a phase factor after one period, imposing the condition
![]()
When shifting the reference point, we can track how ![]() and
and ![]() has transformed:
has transformed:
![]()
Imposing boundaries between the regions. Continuity of the wave function at ![]() requires:
requires:
![]()
As we saw in chapter 4, the derivative of the wave function at ![]() is not continuous, but rather satisfies the condition:
is not continuous, but rather satisfies the condition:
![]()
which leads to:
![]()
If we introduce the dimensionless parameter
![]()
these equations can be written as:
![]()
![]()
Finally, substituting in the Bloch ansatz constrain, we obtain two homogeneous equations in the two unknowns ![]() and
and ![]() .
.
![]()
![]()
The system of equations has a non-trival solution if and only if the determinant is zero, yielding the condition:
![]()
As ![]() , the right hand side of the equation simplifies to:
, the right hand side of the equation simplifies to:
![]()
violating the condition ![]() . This creates a gap where no energy states are allowed. As
. This creates a gap where no energy states are allowed. As ![]() ,
, ![]() , yielding
, yielding ![]() , which oscillates between
, which oscillates between ![]() . These correspond to allowed energy states.
. These correspond to allowed energy states.
![]() versus
versus ![]() . The allowed bands are regions where the curve lies between
. The allowed bands are regions where the curve lies between ![]() and
and ![]() . These regions correspond to values of
. These regions correspond to values of ![]() (and energy
(and energy ![]() ) where solutions exist. Regions where the curve lies outside
) where solutions exist. Regions where the curve lies outside ![]() are energy gaps, meaning that no solution is possible.
are energy gaps, meaning that no solution is possible.

Bands of allowed energies states separated by disallowed energies.
\subsection{Qualitative Features}
Important concepts from earlier chapters.
\begin{itemize}
\item \textbf{Localized wave functions:} A localized wave function means the particle is confined to a particular region of space, such as an infinite potential well where the particle is constrained within the box. Localization implies the probability of finding the particle outside this region is very low.
\item \textbf{Localized wave functions:} A localized wave function means the particle is confined to a particular region of space, such as an infinite potential well where the particle is constrained within the box. Localization implies the probability of finding the particle outside this region is very low.
\end{itemize}
When two wells are far apart (Fig 8.5a), the ground-state energy energy has a two-fold degeneracy since the particle can be in either well. The same conclusion also applies to even and odd wave functions. For ![]() widely separated wells, there are
widely separated wells, there are ![]() degenerate levels. As the wells are brought closer, this
degenerate levels. As the wells are brought closer, this ![]() **degenerates energy level splits into *N* separate energies.
**degenerates energy level splits into *N* separate energies.
Widely Separated Wells
- More explanation: Two potential wells are separated by a large distance. Each well can hold a localized wave function. Consider one well at a time (finite potential well), the electron in the ground-state would have a wave function centered in the well. For two wells, there are two localized ground states: (1) wave function
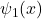 localized in the left well, and (2)
localized in the left well, and (2) 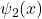 localized in the right well. Both
localized in the right well. Both 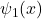 and
and 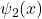 have the same energy because the two wells ae identical. Since there are two possible wave functions corresponding to the same energy level, there is a tww-hold degenracy.
have the same energy because the two wells ae identical. Since there are two possible wave functions corresponding to the same energy level, there is a tww-hold degenracy.
\subsubsection{Wells become closer}
As the wells become closer, the electron’s wave function can no longer be confined to just one well. The wave functions begin to overlap, and the system forms new symmetric (even) and antisymmetric (odd) wave functions, which are linear combinations of the original localized states.
\textbf{{Even Case:} }The even function has less curvature between the wells because it smoothly connects across the barrier. Less curvature means a lower kinetic energy and a lower overall energy.
\textbf{Odd Case:} The odd function has more curvature because it crosses zero (node) between the wells. More curvature means a lower kinetic energy and thus a higher overall energy.
Curvature and kinetic energy:Kinetic energy operator is given by:
Curvature refers to the second derivative![Rendered by QuickLaTeX.com \[T=-\frac{1}{2m}\frac{d^2\psi(x)}{dx^2}\]](http://bootcampforscience.com/wp-content/ql-cache/quicklatex.com-04f0dc25dd9eac59f07e0d7cb0af64f0_l3.png)
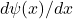 . When
. When 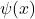 is steep,
is steep, 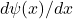 is large and so is the kinetic energy
is large and so is the kinetic energy 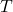 .
.

(a) The wave functions for an electron placed in one or the olher of two widely separated potential energy wells. The even and odd linear combinations of these wave functions, shown in (b), are degenerate in energy. (c) As the separation between the wells decreases, the separation in energy between the even and odd wave functions increases because of the difference in curvature of the two wave functions.

A schematic illustration of how the energy levels for (a) two, (b) three, and (c) N potential energy wells var y with separation of the wells.