Bootcamp for Science

9.2: Binding Energy

Binding energy is the energy required to disassemble a system into its constituent particles. It reflects the stability of the system.

\textbf{Example: A hydrogen atom} When a proton and an electron collide, it forms a hydrogen atom. The binding energy is given by:

(1)   \begin{equation*}E=(m_p+m_e-m_H)c^2\end{equation*}

Semi-empirical mass formula: the binding energy per nucleon is approximated by:

(2)   \begin{equation*} B.E=a_2A-a_2A^{2/3}-a_3\frac{Z^2}{A^{1/3}}-a_4\frac{(Z-\frac{A}{2})^2}{A}+\frac{a_5}{\sqrt{A}}\begin{bmatrix}1 \\ 0 \\ -1\end{bmatrix} \end{equation*}

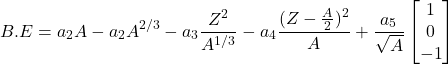
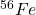  • ^{56}Fe is the most energetically stable atom.
  • Fission: Heavy nuclei (e.g., uranium) release energy when split into smaller fragments.
  • Fusion: Light nuclei (e.g., hydrogen) release energy when combined.

Liquid Drip Model

The liquid drop model approximates the nucleus as an incompressible fluid droplet. It explains the first three terms of the semiempirical mass formula.

Some assumptions of the model are:

  • Nucleons behave like molecules in a droplet.
  • Strong force is short range, so nucleons (protons and neutrons) only interact with nearby neighborhoods.
  • Like molecules in a liquid, nucleons are tightly packed but can move freely.
  • nucleons tend to be spherical to minimize surface area
  • Surface effects matter:

The nucleons on the surface have fewer neighbors and less binding energy than those on the interior.

(3)   \begin{equation*}B.E=a_2A-a_2A^{2/3}-a_3\frac{Z^2}{A^{1/3}}+\text{other terms}\end{equation*}

The first term a_1A is the volume term.

  • The first term can be understood as: each nucleon contributes equally to the binding energy.
  • This is because binding energy is directly proportional to nucleon number 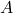A in the nucleus. Moreover, the number of nucleons is proportional to the total volume of the nucleus.

The second term is the surface term:

  • The second term is correct to the first term. Surface nucleons have fewer bonds than interior nucleons, so some energy is subtracted. The nucleus is spherical, so

    (4)   \begin{equation*} \text{surface area}\propto R^2 \propto A^{3/2} \end{equation*}

    Recall that radius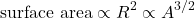 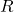R is given by (see Eq(1)):

        \[R=r_0A^{1/3}\]

The third term is the Coulomb term:

  • Electrostatic force (Coulomb force) is long-range. Proton-proton repulsion weakens binding. Electrical energy by the repulsion is given by:

    (5)   \begin{equation*}E_{Coulomb}\propto \frac{Z^2}{R}\propto\frac{Z^2}{A^{1/3}}\end{equation*}

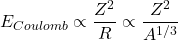
  • The model works because the attractive strong nuclear force is much stronger than Coulomb repulsion. However, surface and Coulomb effects become more significant for larger nuclei.

Fermi Model

The Fermi gas model is a quantum approach to understanding nucleon behavior in the nucleus. It treats proton and neutron as independent fermions moving in a potential well.

  • Solid line: It represents 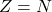Z=N, meaning equal number of protons and neutrons.
  • Dotted points: Actual stable nuclei from experimental data.

For light nuclei, the most stable nuclei lie close to the Z=N line. This suggests a balance between protons and neutrons is energetically favored. For heavier nuclei, the stable nuclei lie below the line, meaning more neutrons than protons are required.

The actual curve deviates because Coulomb’s repulsion between protons increases. The offset the repulsion and maintain nuclear stability, more neutrons are needed. Neutrons help provide attractive nuclear force without contributing to the repulsive electric force.

 

In free space, neutrons are not stable because of beta decay. The neutron decays into a proton, an electron, and an electron anti-neutrino with a lifetime of fifteen minutes.

(6)   \begin{equation*} n\rightarrow p+e^{-}+\bar\nu_e \end{equation*}

This happens because the free neutron is heavier than the proton + electron system. The real question is why neutrons in the nucleus don’t decay. To answer the question, we need to use quantum mechanics in our modeling process.

In the Fermi gas model, nucleons are treated as moving fermions in a 3D potential energy well that confines these particles in the nucleus.

(7)   \begin{equation*}E_F=\frac{\hbar^2}{2m}\Big(\frac{3\pi^2N}{V}\Big)^{2/3}\end{equation*}

The total kinetic energy of the fermions is:

(8)   \begin{equation*} E_{total}=\frac{3}{5}NE_F \end{equation*}

The nucleus is constituted by Z protons and N=A-Z neutrons. The total energy is given by:

(9)   \begin{equation*}E_{total}=\frac{3}{5}Z\frac{\hbar^2}{2m}(\frac{3\pi^2Z}{V})+\frac{3}{5}N\frac{\hbar^2}{2m}(\frac{3\pi^2N}{V}) \propto Z(\frac{Z}{V})^{2/3}+N(\frac{N}{V})^{2/3}\end{equation*}


Assuming V\propto A (volume is proportional to mass number), we get:

(10)   \begin{equation*}(\frac{Z}{V})^{2/3}=(\frac{Z}{kA})^{2/3}\propto\frac{Z^{2/3}}{A^{2/3}}\end{equation*}


(11)   \begin{equation*}(\frac{N}{V})^{2/3}=(\frac{Z}{kA})^{2/3}\propto\frac{Z^{2/3}}{A^{2/3}}\end{equation*}

 

Then, the total energy is:

(12)   \begin{equation*}E_{total}\propto \frac{1}{A^{2/3}}[Z^{5/3}+(A-Z)^{5/3}]\end{equation*}

To find the minimize energy, we differentiate with respect to Z

(13)   \begin{equation*}\frac{\partial E_{total}}{\partial Z}=\frac{1}{A^{2/3}}[Z^{2/3}-(A-Z)^{2/3}]=0\end{equation*}

This gives us:

(14)   \begin{equation*}\boxed{Z=A-Z\rightarrow Z=N=\frac{A}{2}}\end{equation*}

We define

(15)   \begin{equation*}Z=\frac{A}{2}+\delta Z\end{equation*}

We calculate the extra energy \delta E comparing the energy in this new Z with that in Z=A/2:

    \[\delta E\propto\frac{1}{A^{2/3}}\Big [\Big(\frac{A}{2}+\delta Z\Big)^{5/3}+\Big(\frac{A}{2}-\delta Z\Big)^{5/3}+2\Big(\frac{A}{2}\Big)^{5/3}\Big]\]

For small \delta Z/A<<1, we Taylor expand to get leading term:

    \[\boxed{\delta E\propto\frac{(\delta Z)^2}{A}=\frac{(Z-A/2)^2}{A}}\]

This is the asymmetry term in the semi-empirical mass formula. It reflects the extra energy cost of having different numbers of protons and neutrons.