Discrete Random Variables
Discrete random variables take a finite number of values. For instance, the number obtained when throwing a die(1, 2,3, 4,5,6). It is not possible to get values like 5.1, 5.2, etc. Let ![]() be a discrete random variable that takes value
be a discrete random variable that takes value ![]() with probability
with probability ![]() , the sum of probability of every outcome adds up to one.
, the sum of probability of every outcome adds up to one.
(1) ![]()
The mean or expected value of ![]() is:
is:
(2) ![]()
The average of any function ![]() is equal to
is equal to
(3) ![]()
The mean squared value of ![]() is defined as
is defined as
(4) ![]()
Note that ![]() .
.
Example (3.2)
Let x take values 0, 1, and 2 with probabilities 1/2, 1/4, and 1/4 respectively. Calculate ![]() and
and ![]()
Solution
Recall that the expected value of a function is equal to
![]()
![]()
![]()
![]()
Continuous Probability Distribution
Continuous random variables can take a range of possible values. Examples include the length of time spent in a waiting room, where the quantity is not restricted to a finite set of values. The waiting time can be ![]() , or
, or ![]() . The sum of probability is equal to one
. The sum of probability is equal to one
(5) ![]()
The mean is defined similar to 2, expecting that we are now integrating over a continuous region instead of adding over discrete values.
(6) ![]()
For any arbitrary continuous function ![]() , the mean value is
, the mean value is
(7) ![]()
The mean square value is defined as
(8) ![]()
Example(3.3): Guassian
Let ![]() where
where ![]() and
and ![]() are constants. This probability is illustrated in Fig. 3.2 and this curve is known as a Gaussian. Calculate
are constants. This probability is illustrated in Fig. 3.2 and this curve is known as a Gaussian. Calculate ![]() and
and ![]() given this probability distribution.
given this probability distribution.
Solution
Before finding the expected value, the first thing to ensure that the probabilities sum to one is to ensure, allowing us to find the value of constant ![]() . Evaluating the total probabilities, we get:
. Evaluating the total probabilities, we get:
![]()
Solving for
![]()
The mean of
![]()
There are two ways to evaluate the integral. One way is to use the symmetric argument of a even/odd function. Another way is to solve the integral explicitly.
- Symmetric argument: Substituting into the integrate
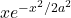 , one can see that
, one can see that 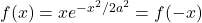 , indicating an odd function. Evaluating the integral over
, indicating an odd function. Evaluating the integral over  , the leftward part of the curve (when
, the leftward part of the curve (when  ) is below the
) is below the 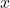 -axis, and the rightward part of the curve when
-axis, and the rightward part of the curve when 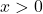 is above the
is above the 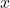 -axis. Both parts have the same area under the curve, except one is negative and one is positive. Adding up the two regions, the total “area” is zero.
-axis. Both parts have the same area under the curve, except one is negative and one is positive. Adding up the two regions, the total “area” is zero. - Solve explicitly: Using u-substitution, we get
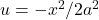 and
and 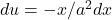 . The integral can be rewritten as:
. The integral can be rewritten as:
(9)
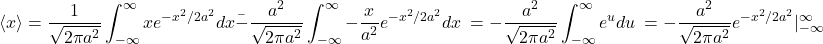
The exponent term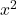 is always positive, so as
is always positive, so as 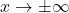 ,
, 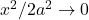 . Evaluating the integral, we get
. Evaluating the integral, we get
The exponent term![Rendered by QuickLaTeX.com \[\langle x\rangle= \frac{1}{\sqrt{2\pi a^2}}\int ^\infty_{-\infty} xe^{-x^2/2a^2}dx = 0\]](http://bootcampforscience.com/wp-content/ql-cache/quicklatex.com-93570dba93ec1cdb42159da00eb0a281_l3.png)
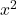 is always positive, so as
is always positive, so as 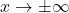 ,
, 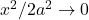 . Evaluating the integral, we get
. Evaluating the integral, we get![Rendered by QuickLaTeX.com \[\langle x\rangle= \frac{1}{\sqrt{2\pi a^2}}\int ^\infty_{-\infty} xe^{-x^2/2a^2}dx = 0\]](http://bootcampforscience.com/wp-content/ql-cache/quicklatex.com-93570dba93ec1cdb42159da00eb0a281_l3.png)
\end{enumerate}
The square mean value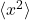 is computed using
is computed using![Rendered by QuickLaTeX.com \[\langle x^2\rangle = \int^\infty_{-\infty} Cx^2e^{x^2/2a^2}= \frac{1}{\sqrt{2\pi a^2}}\int^\infty_{-\infty} x^2e^{x^2/2a^2}\]](http://bootcampforscience.com/wp-content/ql-cache/quicklatex.com-e19626e7070138ff2a68ff0a37093ac2_l3.png)
We solve the integral using integral by parts. Let , we get
, we get![Rendered by QuickLaTeX.com \[u=x, \quad dv=xe^{-x^2/2a^2}dx, \quad du=dx, v=-a^2e^{-x^2/2a^2}\]](http://bootcampforscience.com/wp-content/ql-cache/quicklatex.com-65943cd6a6c71e2a6635861f11425b41_l3.png)
Then, the integral is equal to![Rendered by QuickLaTeX.com \[\frac{1}{\sqrt{2\pi a^2}}\Big([-xe^{-x^2/2a^2}]^\infty_{-\infty}-\int^\infty_{-\infty}-a^2 e^{x^2/2a^2}dx\Big) =\frac{1}{\sqrt{2\pi a^2}} \Big (a^2\int^\infty_{\infty}-e^{x^2/2a^2}dx\Big) = =\frac{1}{\sqrt{2\pi a^2}} a^2\Big (\int^\infty_{\infty}-e^{x^2/2a^2}dx\Big)\]](http://bootcampforscience.com/wp-content/ql-cache/quicklatex.com-e4b4ec1c10db0dd0bf3cef6d5b703235_l3.png)
Does the integral look familiar? It is equal to sum of probability evaluated in part (a) multiplied by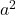 . From (a), we know that the sum of probability is equal to 1. Then, integral for
. From (a), we know that the sum of probability is equal to 1. Then, integral for 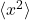 is equal to
is equal to![Rendered by QuickLaTeX.com \[\langle x^2\rangle = a^2\]](http://bootcampforscience.com/wp-content/ql-cache/quicklatex.com-b857a9b4a860a842c209c2d7c0b98454_l3.png)
Linear Transformation
Let ![]() , the average value of
, the average value of ![]() is given by
is given by
(10) ![]()
Example: Linear Transformation
Temperatures in degrees Celsius and degrees Fahrenheit are related by ![]() . Given that the average annual temperature in New York is
. Given that the average annual temperature in New York is ![]() , convert the temperature to degree Celsius using.
, convert the temperature to degree Celsius using.
Solution
We know that
![]()
Then,
![]()
Variance
We quantify the spread of values in a distribution by considering the deviation from
the mean for a particular value of ![]() , defined as
, defined as
(11) ![]()
The quantity tells us how much a particular value is above or below the mean value. Using linear transformation, the average of the deviation for all values of ![]() is:
is:
(12) ![]()
Variance ![]() is defined as
is defined as
(13) ![]()
where ![]() is defined as the standard deviation and is the square root of the variance. The stand deviation presents the root mean square (rms) scatter in the data. A useful identity is:
is defined as the standard deviation and is the square root of the variance. The stand deviation presents the root mean square (rms) scatter in the data. A useful identity is:
(14) ![]()
Independent Variables
If ![]() and
and ![]() are independent variables, the probability that
are independent variables, the probability that ![]() is in the range of
is in the range of ![]() and
and ![]() is in the range of
is in the range of ![]() is given by
is given by
(15) ![]()
The average value of the product is
\begin{euqation}
\langle uv \rangle = \iint P_u(u)duP_v(v)dv
\end{euqation}
Because ![]() and
and ![]() are independent,
are independent, ![]() is a function of
is a function of ![]() only, and
only, and ![]() is a function of
is a function of ![]() only. Then, the double integral can be rewritten as:
only. Then, the double integral can be rewritten as:
(16) ![]()
Because integrates separate for independent random variables, the average value of the product of ![]() and
and ![]() are the product of their average values.
are the product of their average values.
Binomial Random Variables
A binary variable is a variable that has two possible outcomes. For example, sex (male/female). The binomial distribution is a special discrete distribution where there are two distinct complementary outcomes: “success” and “failure”. The distribution is the discrete probability distribution ![]() of getting
of getting ![]() successes from
successes from ![]() independent trials. \
independent trials. \
Suppose that there are ![]() trails, with a probability of success
trails, with a probability of success ![]() . If there are
. If there are ![]() trails of success, the number of trails for failure is
trails of success, the number of trails for failure is ![]() , and the probability of failure is (
, and the probability of failure is (![]() . The number of ways of getting
. The number of ways of getting ![]() success from
success from ![]() trials is given by
trials is given by ![]() . Then, the probability of
. Then, the probability of ![]() trials of success and
trials of success and ![]() trials of failure is
trials of failure is
(17) ![]()
Since the binomial distribution is the sum of n independent Bernoulli trials, then
(18) ![]()
Example (3.9)
Coin tossing with a fair coin. In this case ![]() . Calculate the expected number of heads for
. Calculate the expected number of heads for ![]() and for
and for ![]() .
.